Russian
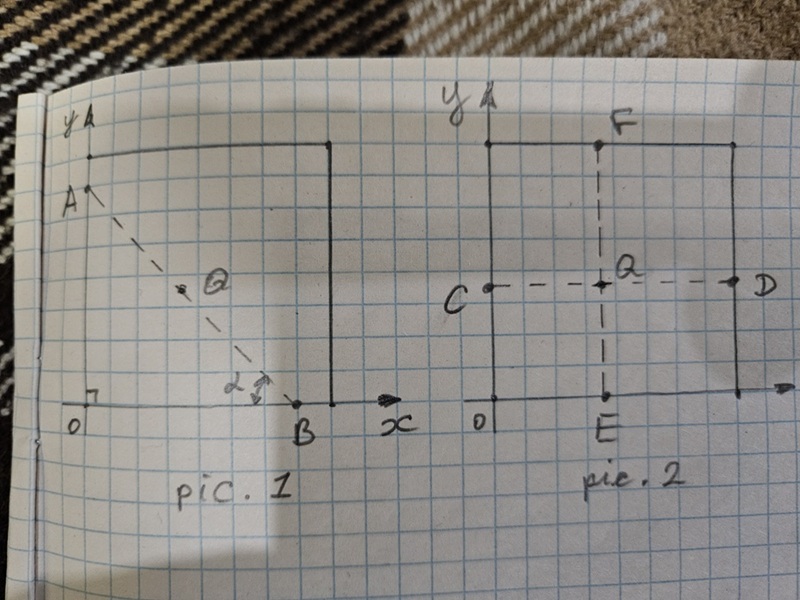
 Поставим ферзя в центр шахматной доски, и также как и в задаче с конём, применим алгебру и геометрию для описания всех возможных ходов. Ферзь ходит по горизонтальной, вертикальной прямым и диагоналям, которые, в свою очередь, являються прямыми линиями. Все эти прямые проходят через точку текущей позиции ферзя. Уравнение прямой описываеться уравнением:
y(x)=a×x + b (1)
При этом ходы на pic. 2 будут описаны такими уравнениями, исходя из (1):
y(x) = b (2)
x(y) = c (3)
 При ходах по диагоналям на pic. 1, вычислим значение a из (1). a являеться производной уравнения (1) или
тангенсом угла ∠ABO (α) равнобедренного прямоугольного треугольника AOB на pic. 1. α = 45° tan45°=1, т.е. уравнения диагоналей будут:
y(x)=x+b (4)
y(x)=-x+b (5)
Теперь используя рекурсию и уравнения 2-5 найдём решение(я).

English
 I place the queen in the middle of a chess board to calculate all possible moves and see it from the point of algebra and geometry.
The same way I did in the knight problem. The queen's moves lied on horizontal, vertical and diagonal lines. All these lines include the current queen's position. The equation describes a line can be written:
y(x)=a×x + b (1)
The moves from pic. 2 can be written:
y(x) = b (2)
x(y) = c (3)
 I need to calculate a from (1) for diagonal moves on pic. 1. a is derivative for the equation (1) or
tangent of the angle ∠ABO (α) from the right isosceles triangle AOB in pic. 1. α = 45° tan45°=1, so the diagonal lines equations will be
y(x)=x+b (4)
y(x)=-x+b (5)
Then using recursion and equations 2-5 I can find solution(s).